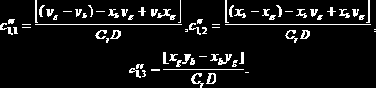CIE.

Если имеется один контрольный цвет, то с помощью него можно получить некоторые цвета, варьируя данный контрольный по светлоте (при условии, что не используется цветовой тон и насыщенность). Данная процедура называется фотометрией и используется при создании монохроматических репродукций цветных изображений.

С помощью двух контрольных цветов можно получить гораздо больше цветов, но не все. Для получения видимого набора цветов используют три контрольных цвета, соблюдая условие, что они находятся в разных областях спектра. Рассмотрим следующий базис цветов:

Red- красный; лежит в области длинных видимых волн (`700 нм).

Green- зеленый; лежит в области средних видимых волн (`546 нм).

Blue- синий; лежит в области средних коротких волн (`436нм).

Рассмотрим цвет C:

r, g, b- относительные количества потоков базовых цветов, входящие в интервал [0; 1]. Но данным сложением можно уравнять не все цвета. Например, для получения сине-зеленого цвета объединяем синий и зеленый потоки цвета, но их сумма выглядит светлее, чем необходимый. Если попытаться сделать его темнее с помощью красного, то получим еще более светлый результирующий цвет, так как световые энергии складываются. То есть мы можем добавлять красный, для получения более светлого образца. Математически добавление красного цвета к поучаемому цвету соответствует вычитанию его из двух оставшихся базовых потоков (физически это невозможно, так как отрицательной интенсивности света не существует). Запишем уравнение следующим образом:

На рисунке показаны функции r, g, b уравнения по цвету для монохроматических потоков цвета с длинами волн 436, 546, 770 нм. С их помощью можно уравнять все длины волн видимого спектра. На графике присутствует отрицательная область. Значения в данной области соответствуют «добавлению»

инструментального цвета к синтезируемому. Изучением данных функций занимается колориметрия. Замечено, что один и тот же цвет можно получить разными наборами базисных цветов (r1, g1, b1) и (r2, g2, b2). То есть цвет можно уравнять различными составными источниками с неодинаковым спектральным распределением. (r1, g1, b1) и (r2, g2, b2)- метамеры.

Представим цвет С как вектор с составляющими rR, gG, bB. Пересечение вектора C

с единичной плоскостью R+G+B=1 дает относительные веса его красной, зеленой и синей составляющих. Их также называют значениями или координатами цветности:

Заметим,

. Рассмотрим связь:

. Если функции уравнивания по цвету перенести в трехмерное пространство, то результат не будет целиком лежать в положительном октанте.

В 1931 был принят стандарт CIE (Commission International de l’Eclairage - Международная комиссия по освещению), в качестве основы которого был выбран двумерный цветовой график и набор из трех функций реакции глаза, исключающий отрицательной области и удобный для обработки. Гипотетические цвета CIE - X, Y и Z.

Треугольник XYZ задан так,

что в него входит видимый спектр. Координаты цветности CIE (x, y, z) задаются следующим образом:

. При проецировании треугольника XYZ на плоскость (x, y) получаем цветовой график CIE. Координаты x и y - относительные количества трех основных цветов XYZ, требуемых для составления нужного цвета. Яркость определяется величиной Y, а X и Y подбираются в соответствующем масштабе. Таким образом, триада (x, y, Y) задает цвет. Обратное преобразование имеет вид:

Комиссия решила ориентировать треугольник XYZ таким образом, что равные количества гипотетических основных цветов XYZ давали в сумме белый. На рисунке изображен цветовой график. Область на графике - видимое множество цветов. На контуре проставлены значения соответствующих длин волн в нм, соответствующие чистым, не разбавленным цветам.

В центре области находится опорный белый цвет - точка равных энергий, с координатами x=y=0.33(3).

Часто применяют следующие источники CIE:

Название	Температура	x	y
Лампа с вольфрамовой нитью накаливания.	2856К	0.448	0.408
Солнечный свет в полдень.	5600К	0.349	0.352
Полуденное освещение при сплошной облачности.	6300К	0.310	0.316
Опорный белый стандарт для мониторов и NTSC.	6400К	0.313	0.329

Система (x, y, Y) подчиняется законам Грассмана. На рисунке показана цветовая область графика CIE.

Как видно, наибольшую площадь занимают цвета с преобладанием зеленого,

что согласуется с чувствительной избирательностью человеческого глаза.

На цветовом графике CIE удобно демонстрировать цветовой охват различных систем и оборудования: телевидения, типографской печати, фотопленок и т.п. Цветовой обхват для аддитивных систем - треугольник с вершинами, соответствующими основным цветам RGB.

Цвет, который можно получить в данной цветовой модели лежит внутри треугольника, цвета, лежащие вне - получить невозможно. Примеры цветовых обхватов для некоторых моделей можно увидеть на рисунке. Заметим, что для цветной пленки обхват есть криволинейный треугольник. Причина этого заключается в нелинейном (в данном случае логарифмическом) законе создания цветного изображения с помощью цветной пленки. Ниже приведена таблица основных цветов моделей в координатах цветового графика CIE:

Модель	Цвет	x	y
CIE XYZ.	Красный Зеленый Синий	0.735 0.274 0.167	0.265 0.717 0.009
Стандарт NTSC.	Красный Зеленый Синий	0.670 0.210 0.140	0.330 0.710 0.080
Цветной монитор.	Красный Зеленый Синий	0.628 0.268 0.150	0.346 0.588 0.070

Координаты цветности CIE представляют точный стандарт определения цвета. Координаты цветности CIE полезны при передаче цветовой информации из одной цветовой модели в другую. Поэтому необходимо знать преобразование координат CIE в другие цветовые модели, а также и обратно.

Например, преобразование RGB - CIE XYZ задается следующей формулой:

,где

- цвета для получения координаты единичного основного цвета R, аналогично и для G и B. Если известны координаты цветности CIE x и y

для основных цветов RGB, то: